Solving big problems on small computers

Ever since I started studying bioinformatics it was always hard to explain to people what exactly a bioinformatician does, after all, truly grasping the concept of bioinformatics requires both at least some understanding about informatics and computational biology. The easy answer always has been "Yeah, I am solving some medical problems on the computer", however, that hardly paints the correct picture. Nowadays even more so. I think most of my friends actually have no idea what I am doing for a living, despite just nodding in acknowledgement whenever I try to explain. In this blog post I want to go into a bit more details what I have been up to over the past year.

Disclaimer: This whole blog post is based on a presentation I gave earlier this year. If you want to see me talk live about science stuff, check out "Micha Birklbauer: Tour Dates".

Most of you probably know (or have at least heard) that I am doing research in the field of protein-protein cross-linking, and more specifically, write software for the identification of crosslinks from mass spectrometry data. Now, to explain what all that means we have to start with the basics - or rather with mass spectrometry-based proteomics (which is not so basic but necessary for understanding cross-linking). For the sake of understanding I will drastically simplify everything in this blog post, so please don't come at me and scream "Fake News" if any of the things are not exactly as described in established literature. For those of you who really want to get down to business, I can recommend this review on bottom-up proteomics that explains everything in-depth: Comprehensive Overview of Bottom-Up Proteomics Using Mass Spectrometry.

But let's try to paint this in simpler strokes: Proteins are the building blocks of life, they control basically everything that happens in our bodies. Mass spectrometry-based proteomics is all about studying these proteins, more specifically identifying and quantifying proteins in samples of interest. Imagine you are taking a blood sample from a patient and you want to know which proteins are in there, you can analyze the sample with a mass spectrometer which does some magic and it will give you some data (the mass spectra) in return. However, now comes the tricky part (not saying that the previous steps are not also complicated, but I am not really involved with that so I won't focus on it), the mass spectra don't directly tell us which proteins are in our sample, we need software that can do that!

You can imagine this problem of identifying proteins from these mass spectra as a big game of memory - you know, the game where you have to find two identical cards. Except that instead of 10 - 20 pairs it's more like ten thousand to a few million pairs, they don't exactly match and there might not be a pair for every card and for some cards there might be multiple. Not so easy anymore, I guess. How this exactly works is that we can take all known proteins that are encoded by the human genome and we can more or less calculate how a mass spectrum for parts of them might look like. Subsequently, what's left is that you compare your experimentally measured mass spectra to the calculated ones and if you find something that matches really well, chances are good that this is one of the proteins in your sample! Pretty cool, huh? My supervisor wrote a software that does exactly that, except of course in a way more sophisticated way which is why it performs really, really well. You can read more about that here: MS Amanda.

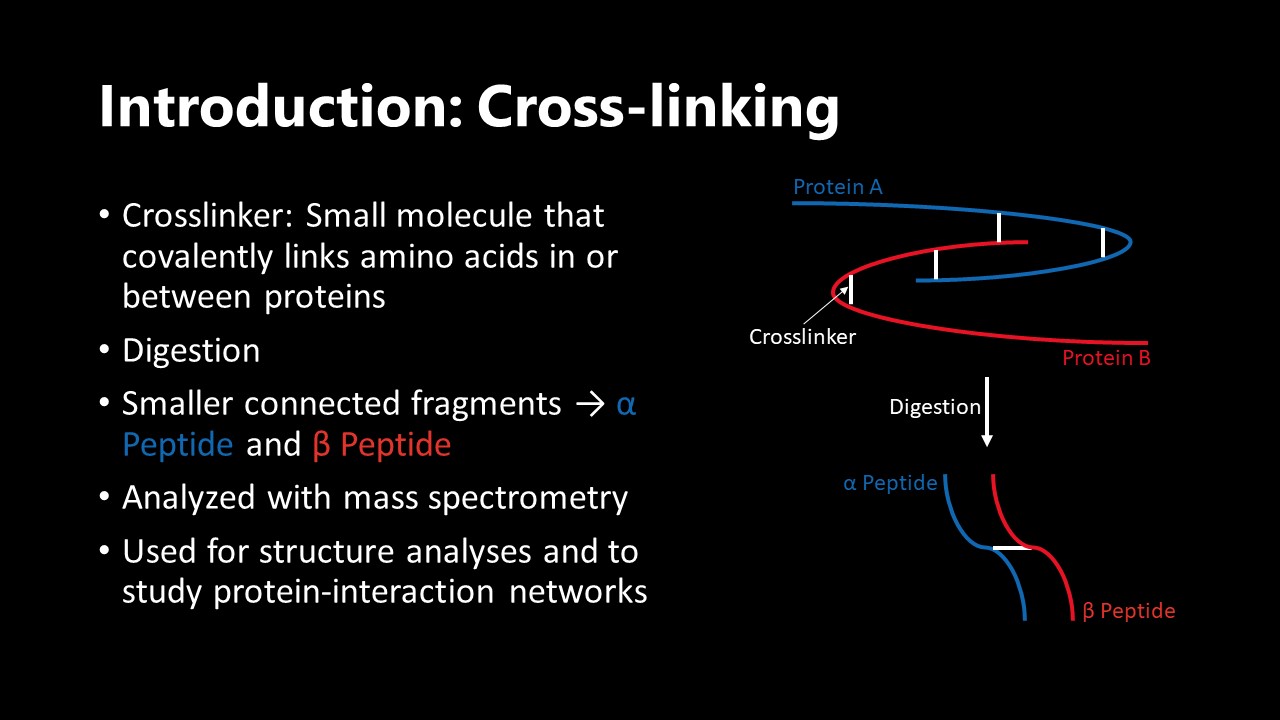
In cross-linking mass spectrometry the question is less about which proteins are in the sample but more about which proteins interact in our sample. This is facilitated by adding a chemical reagent called the crosslinker to your sample, which you can imagine like a chain that connects two proteins that are close enough together. The tricky part in analyzing mass spectra from cross-linking experiments is that instead of having (parts of) one protein in your spectrum, you suddenly have (parts of) two proteins in your spectrum that are connected by this chain (crosslinker)(you can read more about cross-linking here: Cleavable Cross-Linkers and Mass Spectrometry for the Ultimate Task of Profiling Protein–Protein Interaction Networks in Vivo). Now that is where my work is coming in, my project is about writing software that can tell you exactly that: Looking at a mass spectrum, which (parts of) proteins are in there and connected (and therefore interact with each other)?

You can see a graphical depiction of cross-linking below. Usually the two connected parts of the protein(s) are called the alpha and beta peptide - where "peptide" refers to a smaller fragment of a protein.

In classical bottom-up mass spectrometry-based proteomics we usually know the mass of the particular peptide that we look for in a mass spectrum. This drastically simplifies the identification process as we only have to consider peptides with a similar mass from our database. Contrary, in cross-linking - or more specifically - in non-cleavable cross-linking, which uses a distinct kind of cross-linking reagent, we only know the mass of the whole cross-linked entity but not the mass of the individual peptides.

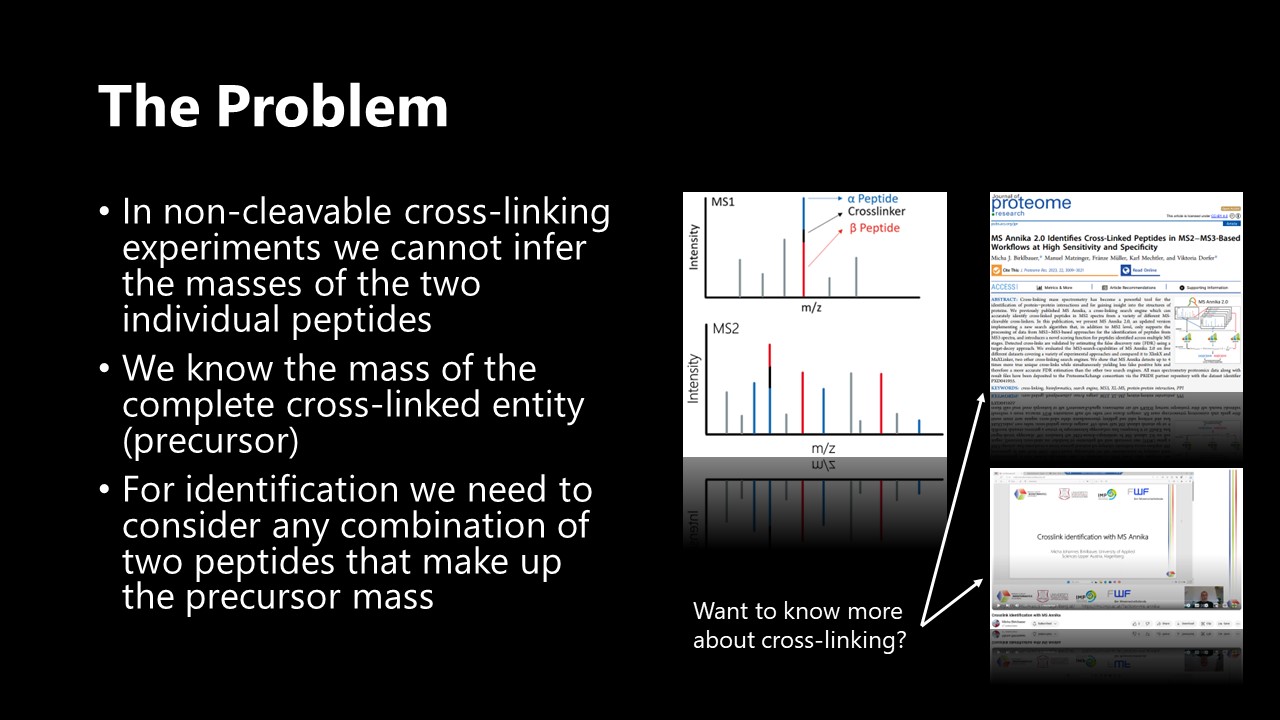
Identification therefore becomes a combinatorial problem as we now have to consider every combination of peptides in our database. For a database of n peptides the number of combinations c to consider can be calculated as follows:

For large n this problem can be regarded as O(n²) complexity, hence why this is usually referred to as the n-squared problem in cross-linking.

If we consider the human proteome as our protein database, the number of peptides is around 2 749 058 and when you plug this number into the formula above you get 3 778 661 318 211 possible combinations. This is already a very large number that we can hardly imagine anymore. If you were to store all of these combinations on a computer using a very simple data structure consisting of two 32-bit integers to denote the two peptides and one 64-bit integer for the index you would end up with almost 55 terabytes (TB) of storage needed. For funzies I put a picture below what that would mean in terms of hardware requirements to store such an amount of data.

Needless to say that this is unfeasible. Over the past year I have now been working on how to solve this problem and bring identification of non-cleavable crosslinks to everyone! 😉

Approaching problems like this always starts with going through the five stages of grief and crying is probably just part of doing a PhD. Anyway, after you reach acceptance it's time to stop breaking down and start breaking down the problem and searching for solutions. It was very obvious that in this case the "solution" would be, on the one hand to limit the number of combinations, and on the other hand to implement a very fast search algorithm that can deal with a high number of combinations. Both of these things are easier said than done, after all there is a reason why this challenge has still mostly remained unaddressed after all these years of non-cleavable cross-linking - which is also why non-cleavable cross-linking has been limited to small scale experiments.

Let's start with the problem of limiting the number of combinations to consider for identification: If only we could identify one of the two cross-linked peptides, the number of possible combinations that we need to address would shrink to n instead of n-squared. Therefore, to-do number one: Identify one of the two peptides.

Secondly, implementing a search algorithm capable of processing very large amounts of combinations: This was less straightforward, I remember that back then I was thinking about which technologies have been super optimized over the past decades and which of them I could maybe apply to the problem at hand. My initial gut feeling was to break down the search into a process of matrix multiplications, an operation which is highly optimized, very widely adopted in computer science and also drives today's artificial intelligence hype. Moreover, today's compute devices easily can handle matrices with several thousands if not millions of rows and columns, ideal for processing large numbers of combinations.

The question remained, how would you represent peptides and mass spectra as peptides? For that I'd recommend reading the pre-print which explains this in detail.

Like all ideas this one also started on paper, you can see the first draft below! The core idea of the algorithm is still the same today, even though many parts changed from its inception to the final implementation that is now incorporated in MS Annika 3.0 - the crosslink search engine I am developing. I'll go over the final implementation of the algorithm towards the end of this blog post, but for now I want to focus on the journey of how I got there!

After pitching the idea to my supervisor and agreeing that it was worth a try, the next step was to think about the technical implementation which essentially boiled down to the question of how to do the matrix multiplication. Now to put this into perspective, it is worth noting that MS Annika - the crosslink search engine we already built - is implemented in C# because it functions as a plugin node for Thermo Fisher's mass spectrometry software called Proteome Discoverer. However, C# is a managed language that is unfortunately not the fastest, meaning there were several things to consider:

• Use a C# native matrix multiplication: Easy to implement and easy to interface with the already available MS Annika code, but probably at the cost of performance
• Use a matrix multiplication implementation that is not C# native: Potentially much faster but interfacing with the existing MS Annika codebase might be a problem

I ended up testing several different approaches (as outlined below), both in C# and other languages.

Let's start off with the C# native implementations, the first thing I tested was a numeric algebra library called Math.NET: Now Math.NET was quite straightforward to use, supported sparse matrices out of the box and was very easy to integrate into the existing MS Annika code. For smaller matrices it also performed decently well, however - as already mentioned - small matrices were not a comfort we were allowed to have. The goal was to solve problems consisting of matrices that were very large and for that Math.NET unfortunately was way to slow. The identification process using a simulated human proteome database and one single simulated mass spectrum would take more than 40 seconds, which is way too long considering that studies of that scale usually feature several hundred thousand mass spectra.

The next library I took into consideration was ALGLIB. The report for this is going to be a short one: I simply couldn't get it to run. Moreover, in retrospective I don't even know why I even tried - even though it's an established library, it's a commercial solution and in the free version only supports single threaded computation. Big nono!

The last C# native approach was using the vector implementation of the standard library in System.Numerics.Vector. This was doomed from the start and if only I would have read the documentation first, I would have saved myself the time of even trying this method. Turns out that System.Numerics.Vector only supports up to 4 dimensions, which is obviously way too little for our purpose. In conclusion, it was pretty clear that the matrix multiplication has to be done in some other language not within the .NET framework.

I have always loved Julia (the programming language), in my opinion it does a lot of things right as a programming language + it is super-fast in many ways. Julia also has a great reputation when it comes to numerical computing, so I was eager to give it a try for my matrix multiplication problem. Writing a matrix multiplication in Julia is also really easy, especially when it comes to setting up random matrices for testing purposes. It features a standard library called SparseArrays that comes with implementations for sparse matrices and sparse matrix multiplication. In fact, the code for testing if Julia was fast enough for my problem at hand can be written down in six lines of code:

#!/usr/bin/env -S julia --color=yes --startup-file=no
using SparseArrays
function SpMV(rows::Int64 = 1000000, cols::Int64 = 500000)
    M = sprand(Int8, rows, cols, 0.0001)
    V = sprand(Float64, cols, 1, 0.002)
    return @time M * V
end

Calling the function SpMV would initiate a random sparse matrix with 1 000 000 rows and 500 000 columns, simulating a protein database of 1 000 000 peptides. The density of this matrix was defined as 0.0001 because I assumed a maximum of 100 ions per peptide. The function also initiates a random sparse vector (or rather 1-dimensional sparse matrix) with 500 000 elements of which a fraction of 0.002 are non-zero. This vector denotes one simulated mass spectrum with 1000 peaks. The matrix multiplication would then be timed with @time. And don't worry, this is all the code I am going to share throughout the whole blog post - I just wanted to demonstrate how easy it is!

Turns out that it's true what they say, Julia is actually pretty fast: The above multiplication is calculated in a fraction of a second! Julia also supports mixed compute-types and offloading computations to the GPU with CUDA. Very promising!

But now the bad news: Julia does unfortunately not interopt well with C#, and what I mean with that is not that it's impossible but rather that it's kinda complicated. Me no like that! I tried combining C# and Julia by simply calling the Julia script from C# and it would have been possible to pass data via reading and writing to intermediate files, but in this case disk IO operations would always have been a bottleneck and performance would suffer.

Onto the next thing then…

When all else fails you turn back to your old gods: C and C++. I knew that interfacing C and C++ code with C# would work well because a lot of applications do that. So I went looking for good linear algebra libraries since there was no way I would implement matrix multiplication myself in C or C++ (which I also eventually did, but that is another story). My Austrian heritage prompted me to give ViennaCL a try, but to my disappointment I could not get that to run for my setup. Probably due to my lack of C and C++ experience. Skill issue, I guess. In the end it didn't even matter because I found Eigen - or maybe it was all destiny and Eigen found me - which was a blessing in many ways. Eigen is open-source, has good sparse matrix support, is very fast and memory efficient but also has super nice and helpful developers and community members! Over the past year I have learned a lot about C++ and matrices just from the Eigen community Discord alone and I will always be grateful to all the members who helped debugging messy code snippets and giving advice! Thank you, Eigen community!

Eigen performed at a similar level as Julia (if not even faster) and for GPU computing I ended up going with cuSPARSE directly. If I were to re-do the implementation today, I would maybe consider Rust instead of C++, mostly because of faer. But back then (the good old days when I was still young) things were not as fleshed out as they are today. However, I still am very happy with my choice and do think Eigen was and still is the best tool for the job in my case! With that settled I had to implement the interoperability between C# and C++ which turned out to be another adventure! 😉

Uncle Ben once said "With great ideas come great challenges" or something like that (I completely made that up because I love lying (not in my research though)) and he was absolutely right. Figuring out the matrix multiplication was only one piece (weeb reference) of the puzzle. But turns out that most of my ensuing problems could simply be solved with the ostrich algorithm. Poggers moment. In fact, why would I worry about the performance of mixed compute types when my existing implementation already worked decently well? And who cares about out-of-core operations, if someone loads up the program with more than 21 474 836 peptides maybe they just deserve that crash? I specifically stated this in the limitations by the way, just so you know - I am not being rude here! 😉

What I really needed to solve though was the interoperability between C++ and C#: In .NET that process is called marshalling. Specifically, what I needed to do is to get my matrix from my C# program to my C++ program and then the result back. It is possible to marshal custom data structures but it is much easier to stick to commonly available data types. So basically arrays.

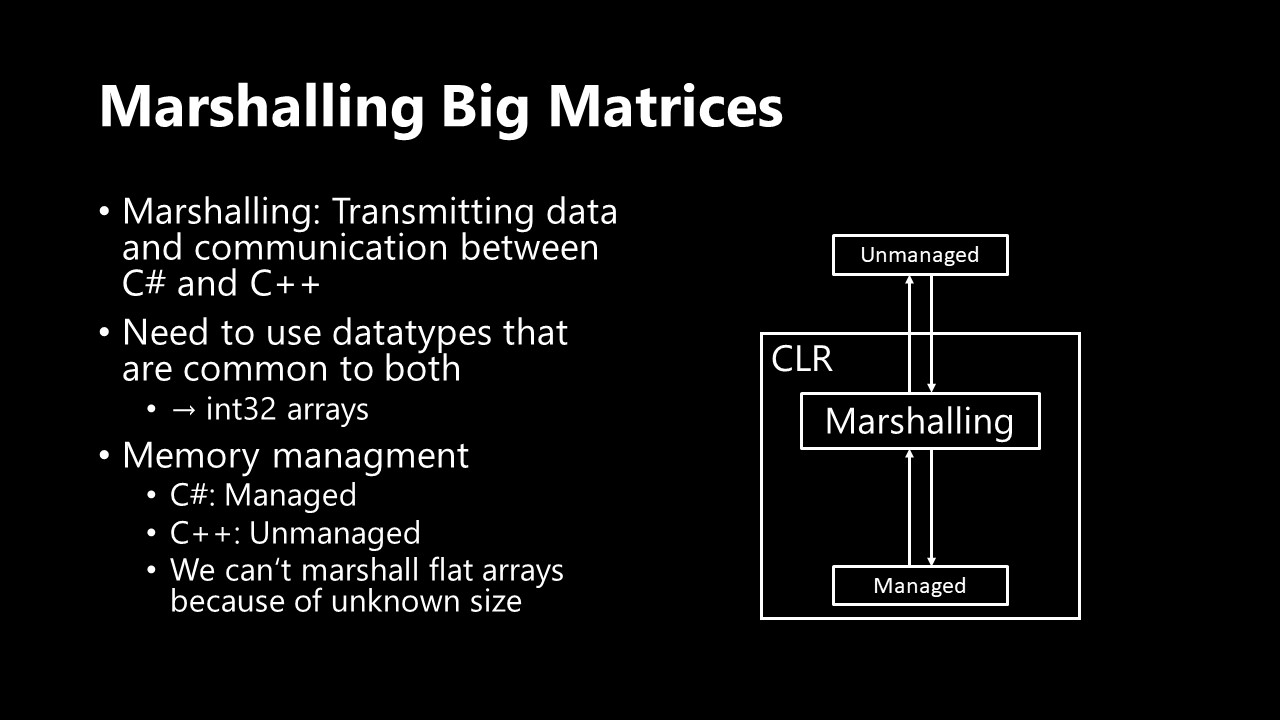
Or rather pointers to arrays because we don't know array size at compile time. That was the point where I really learned something new about C#: Turns out that you can actually do pointers in .NET by telling the garbage collector to pin a specific object to a certain memory address. Whaaat?!

So how do I transform my matrices into arrays? Just creating a flat dense array would not be possible because the size would be too big (that's what she said). Once again, the know-it-all I am, I went into the whole process without reading up on sparse matrix formats. To be honest, usually I am not the kind of guy that doesn't read up on things beforehand, but during this whole project I was so eager on doing things that it was mostly "code first, research later". I do think however that it is kind of funny that when you really put a lot of thought into something, you just end up with the exact same optimal solution that other people already discovered. What a surprise!

My solution was to create two arrays, one would hold all column indices and the other would store information at which indices in the first array a new row starts. Heard that before? Probably not if you aren't into sparse matrices - but that's what's called compressed sparse row format. Well, except I don't have a values array because the matrix values are calculated during matrix initialization. So one could argue that I even invented an optimized version of CSR format. 🤯

With all the technological questions answered, I just needed to address the biological questions - which took another half-year if not more. But I will save you the time and not talk about that - maybe one day in my dissertation. The final algorithm looked like this:

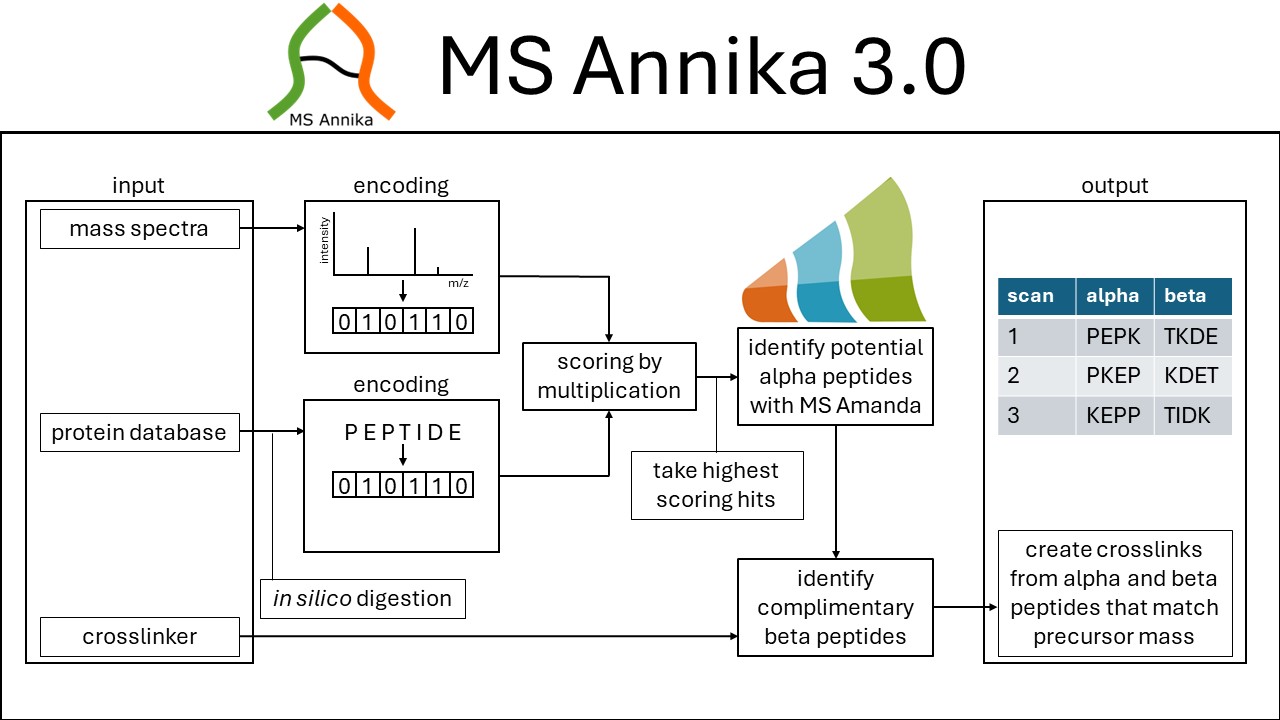
Explanation (as taken from the pre-print): Schematic overview of the algorithm for identification of non-cleavable crosslinks in the search engine MS Annika. Mass spectra and peptides arising from the in silico digestion of the protein database are encoded as sparse vectors and subsequently scored by matrix multiplication. The highest scoring hits are considered for the identification of potential alpha peptides with the peptide search engine MS Amanda. Identified alpha peptides are used to find complimentary beta peptides and ultimately alpha and beta peptides matching the mass spectrum's precursor mass are combined to crosslinks.

After my "fuck around" phase it was time to enter my "find out" era: It was time to multiply some peptide matrices with some mass spectra matrices.

Now to make it short: It worked! It worked well, and I was - still am - actually pretty happy with the results! I - or rather we, my co-authors and I - solved a problem that has been a challenge for years if not decades. And the solution does not require some expensive compute cluster but runs on a normal office laptops. I think that's quite cool!

I am not going to show any of the results because I have done this in detail in the publication, so if you have some biological background and are interested, you can check that out.

All I can say is, I have been chasing the endorphin rush that I had when I saw that this method worked for the first time ever since! 😉

I have learned a lot over the past year, but here are some of the most important things that apply to more areas than just programming which I wanted to share!

Thank you for reading all this! In all seriousness though, this section belongs to all my co-authors and most importantly my supervisor and my co-workers, mostly for putting up with all the nerd-shit^TM I have been throwing around every time I learned something new that fascinated me. Thanks for tolerating me! (And supporting me in all situations and moods, love you guys lots! ♥️)